常见基本回测指标

1 年化收益率

年化收益率是把当前收益率(日收益率、周收益率、月收益率)换算成年收益率来计算的,是一种理论收益率,并不是真正的已取得的收益率.例如日收益率是万分之一,则年化收益率是3.65﹪(平年是365天).因为年化收益率是变动的,所以年收益率不一定和年化收益率相同.

年收益率:一笔投资一年实际收益的比率.
年化收益率:投资(货币基金常用)在一段时间内(比如7天)的收益,假定一年都是这个水平,折算的年收益率.

年化收益率=[(投资内收益/本金)/投资天数]*有效投资时间*100%
年化收益率(单利)=持有收益率/持有时间[年]*100%
年化收益率(复利)=[(1+持有收益率)^(1/持有时间[年])-1]*100%

年化收益=本金×年化收益率
实际收益=本金×年化收益率×投资天数/有效投资时间

1.1 有效投资时间

有效投资时间D是随不同市场而变动的

• 1.像银行存款、票据、债券等一般每年按360天(或很少情况下365天)计息,即D=360天.
• 2.而股票、期货等公开交易市场,其有效投资时间便是一年的交易日数,扣除节假日后约为250日(每年52周,每周5个交易日,一年大约10天节假日: 52×5-10=250)即D=250天.
• 3.对于房地产、普通商业、实业等由于每天都可以买卖或开业,并不受节假日的影响,所以有效投资时间便是一年的自然日数,即D=365天.
• 4.因闰年而导致的个别年份多一天等非常特殊的情况,由于其影响很小,自然可忽略不计

1.2 计算公式

假设:

• (1)投资人投入本金C于市场,经过时间T后其市值变为V;
• (2)D表示一年的有效投资时间

则该次投资中:

1.持有收益为: P=V-C
2.持有收益率为: K=P/C=(V-C)/C=V/C-1
3.年化收益率(单利: 一次性投资)为: 
  (1).Y=(1+K)^N-1=(1+K)^(D/T)-1
  (2).Y=(V/C)^N-1=(V/C)^(D/T)-1
  其中 N=D/T 表示投资人一年内重复投资的次数
4.年化收益率(复利: 连续多期投资)为: Y=(1+K)^N-1=(1+K)^(D/T)-1
  其中: K=∏(Ki+1)-1, T=∑Ti

1.3 单利: 一次性投资

假设投资人在某一时刻投资了本金C于一个市场(比如股市),经过一段时间T后其市值变为V,

则这段时间内投资人的收益(或亏损,如果V<C的话)为P=V-C,

其收益率(即绝对收益率,以下简称收益率)为K=P/C=(V-C)/C=V/C-1,

而假设一年的所有有效投资时间为D,

则投资人可在一年内重复投资的次数为N=D/T,

那么该次投资的年化收益率便可表示为: Y=(1+K)^N-1=(1+K)^(D/T)-1或Y=(V/C)^N-1=(V/C)^(D/T)-1.

• 栗子1:

  假设投资者甲投资1万元(C=1万元),经过一个月后市值增长为1.1万元(V=1.1万元),

  则其收益为P=V-C=0.1万元,即赚了1000元.

  那么其该次投资的收益率为K=P/C=10%,

  由于一年有12个月即一年可以重复进行12次(N=D/T=12),

  同样的投资,所以其年化收益率为Y=(1+K)^12-1=1.1^12-1≈213.84%.即一个月赚10%相当于一年变成2.1384倍,投资者甲反复如此投资的话,1万元本金一年后可以增值到31384元.

  反之,如果很不幸该投资人一个月亏掉了1000元,

  那么该次投资的净收益为P=-0.1万元,收益率为K=P/C=-10%,

  年化收益率为Y=(1+K)^12-1=0.9^12-1≈-71.76%.

  也就是说投资人每个月都亏10%的话,一年后将亏掉本金的71.76%,到年底其1万元本金便只剩2824元了.

• 栗子2:

  假如投资者乙做长线,28月赚了3.6倍,即最初投资的本金1万元两年零4个月后增值到4.6万元.这里该次投资的投资时间为T=28月,

  所以其每年可以重复投资的次数为N=D/T=12/28.

  其该次投资的收益率为K=360%,

  而年化收益率为Y=(1+K)^N-1=4.6^(12/28)-1≈92.33%,也就是接近于每年翻番.

• 栗子3:

  假如投资者乙第二次的长线投资是35个月亏损了68%,即最初投资的1万元本金2年另11个月后只剩下3200元.

  那么其本次投资的时间为T=35月,N=D/T=12/35,

  而收益率K=-68%,

  则年化收益率Y=(1+K)^N-1=0.32^(12/35)-1≈-32.34%,即接近于每年亏损1/3.

• 栗子4:

  再看一个超长期的投资者丙,假设他投资1万元买入的股票26年后增值了159倍至160万元.

  那么其该次投资中T=26年,N=D/T=1/26,

  收益率K=15900%,

  而年化收益率Y=(1+K)^N-1=160^(1/26)-1=21.55%,也就是说其投资水平与另一个一年赚21.55%的投资者相当.

• 栗子5:

  假设投资者丙最初买入的另一只股票18.3年后只剩下5%,即一万元本金亏损到只剩500元,

  那么该次投资中T=18.3年,N=D/T=1/18.3,

  收益率K=-95%,

  而年化收益率则为: Y=(1+K)^N-1=0.05^(1/18.3)-1≈-15.1%.即相当于每年亏损了本金的15.1%.

• 栗子6:

  假如投资者丁在权证或期货等市场上做交易,每天可做多次T+0交易,假设该市场一天交易4小时,

  一年的有效交易时间为D=250日×4小时/天×60分钟/小时=60000分钟.

  假设他某天某时某刻投资1万元开仓,15分钟后平仓赚了108元.

  那么该次交易中T=15分钟,N=D/T=60000/15=4000,

  收益率K=108/10000=1.08%,

  则年化收益率为Y=(1+K)^N-1=1.0108^4000-1≈4.58×10^18!

  既相当于一年赚458亿亿倍！由此可知,交易时间越短的话,即使单次收益的绝对收益很小,但年化收益率都非常非常大,往往变成一个天文数字！

  而假如他另一次交易中37分钟1万元本金亏损了76元的话,

  则该次T=37分钟,

  N=D/T=60000/37≈1621.62,

  收益率K=-0.76%,

  故年化收益率为Y=(1+K)^N-1=0.9924^1621.62-1≈0-1=-100%.

1.4 复利: 连续多期投资

假设投资人用本金C开始,连续进行了n次投资,那么其第i次(i=1～n)投资的情况与上述的单次投资完全一样,

具体可表示为:

第i次投资的期初本金为Ci,

期末市值为Vi,

所耗时间为Ti,

该次投资的净收益为Pi=Vi-Ci,

其收益率为Ki=Pi/Ci=(Vi-Ci)/Ci=Vi/Ci-1.

在没有追加或减少投资资金的情况下,显然每次投资的期末市值等于下一次投资的期初本金,即Vi=Ci+1.

而第一次投资的本金为C1=C.全部n次投资完成后,其净收益P等于每次投资的收益总和即P=∑Pi,投资时间等于每次投资的时间总和即T=∑Ti,而投资收益K=∏(Ki+1)-1.

然后将全部n次投资的结果看作一次投资,使用上面介绍的一次性投资的计算方法,即可简单地计算出该段时间全部n次投资的年化收益率.

• 栗子1:

  假设投资人最初投资1万元本金,第1次3个月赚了50%,账户增值至1.5万元;

  紧接着第二次两个月亏损了40%账户缩水至0.9万元;

  然后马上第三次八个月赚了120%,账户增值至1.98万元.

  则总的来看,投资人最初的1万元经过13个月后增值至1.98万元,

  其净收益为P=0.98万元,

  收益率为K=98%,

  年化收益率为Y=(1+K)^N-1=1.98^(12/13)-1≈87.87%.

  请注意这里每一次的投资净收益分别为0.5万元,-0.6万元和1.08万元,其总收益即为三者之和0.98万元.

  与此同时,三次的收益率分别为50%,-40%和120%,其总的收益率为K=∏(Ki+1)-1=1.5×0.6×2.2-1=98%.

  也就是说在既不追加也不减少本金的情况下,将多次投资的总和全部看成一次投资来计算,其结果与单独计算每一次投资后再合成没有任何差别,当然相比之下前者就是非常简单的方法了.

• 栗子2: 上述例子中,如果三次投资并不是连续的,中间有资金空闲的情况

  假如说第一次卖出后空仓了3.7个月,期间收获税后利息18.62元,

  而第二次投资后在第三次投资前又空仓了2.5个月,期间收获税后利息7.55元,又该如何计算呢？！

  看起来很复杂,其实非常简单！完全可以把两次空仓当作另两次存银行赚取活期利息的投资,这样一来,加上上述的3次投资,不就变成了连续的5次投资了吗？

  总的来说,不就是1万元本金经过19.2个月(13+3.7+2.5=19.2)后增值到19826.17元吗？

  这样收益率K=98.2617%,

  而年化收益率Y=(1+K)^N-1=1.982617^(12/19.2)-1≈53.38%

  其实即使中间没有利息,比如说将钱免息借给朋友一段时间再收回来,也都是一样的.总之,只要将一段考察时间内的总收益K和时间T带入公式Y=(1+K)^N-1=(1+K)^(D/T)-1即可.

• 栗子3: 在投资本金变动的情况下,又如何来计算呢？

  假如投资者进行开放式基金交易,受客户的申购或赎回影响其投资资金量每天不断地发生变动.

  这时候虽然最终的净收益必然也等于每一次的净收益之和,即P=∑Pi,

  投资时间等于连续每期投资的时间之和,即T=∑Ti.

  但由于不断追加或减少投资本金,造成每一次的期末市值并不等于下一次的期初本金,即Vi≠Ci+1.

  这种情况下,便有两种方法来计算年化收益率,第一种是几何平均的方法,即先计算连续每期的收益率Ki,再根据总的收益率K=∏(Ki+1)-1计算出总收益率K,再代入公式Y=(1+K)^N-1=(1+K)^(D/T)-1计算即可.

  在本金大幅度变动的情况下,这种办法可以做到公平而精确地考察和比较投资者的收益水平.

  而在本金变动幅度不是很大的情况下,直接采用期初的本金C和总的净收益P代入公式Y=(V/C)^N-1=(V/C)^(D/T)-1计算即可,其实质是将其简化为没有本金变动的情况.

import pandas as pd
import tushare as ts

start_date='2020-01-01'
end_date='2020-12-16'

# http://tushare.org/trading.html#id2
df=ts.get_hist_data('600519',start=start_date,end=end_date)
rs=(df.head(1)['close'].values[0]/df.tail(1)['close'].values[0])**(250/df.shape[0])-1
print('股票600519的年化收益率=%.2f%s' % (rs*100,'%'))

输出: 
股票600519的年化收益率=69.11%

2 夏普比率

夏普比率(Sharpe Ratio),又被称为夏普指数 — 基金绩效评价标准化指标.夏普比率在现代投资理论的研究表明,风险的大小在决定组合的表现上具有基础性的作用.风险调整后的收益率就是一个可以同时对收益与风险加以考虑的综合指标,长期能够排除风险因素对绩效评估的不利影响.夏普比率就是一个可以同时对收益与风险加以综合考虑的三大经典指标之一. 投资中有一个常规的特点,即投资标的的预期报酬越高,投资人所能忍受的波动风险越高;反之,预期报酬越低,波动风险也越低.所以理性的投资人选择投资标的与投资组合的主要目的为: 在固定所能承受的风险下,追求最大的报酬;或在固定的预期报酬下,追求最低的风险.

2.1 核心思想

夏普指数代表投资人每多承担一分风险,可以拿到几分超额报酬;若大于1,代表基金报酬率高过波动风险;若为小于1,代表基金操作风险大过于报酬率.这样一来,每个投资组合都可以计算Sharpe Ratio,即投资回报与多冒风险的比例,这个比例越高,投资组合越佳.

• 代表投资人每多承担一分风险,可以拿到几分报酬,单位风险所获得的超额回报率
• 该比率越高,策略承担单位风险得到的超额回报率越高

2.2 计算公式

夏普比率=(投资组合预期报酬率-无风险利率)/投资组合超额报酬率的标准差

SharpeRatio=(E(Rp)-Rf)/σp
# E(Rp): 投资组合预期报酬率
# Rf: 无风险利率
# σp: 投资组合超额报酬率的标准差

2.3 举个栗子

假如国债的回报是3%,而您的投资组合预期回报是15%,您的投资组合的标准偏差是6%,那么用15%－3%,可以得出12%(代表您超出无风险投资的回报),再用12%/6%=2,代表投资者风险每增长1%,换来的是2%的多余收益.

import pandas as pd
import numpy as np

year_list=[]
month_list=[]
rtn_list=[]

# 生成对数收益率,以半年为周期
for year in range(2006,2017):
  for month in [6,12]:
    year_list.append(year)
    month_list.append(month)
    rtn=round((-1)**(month/6)*(month/6/10),3)+(np.random.random()-0.5)*0.1
    rtn_list.append(rtn)

# 生成半年为周期的收益率df
df=pd.DataFrame()
df['year']=year_list
df['month']=month_list
df['rtn']=rtn_list

# 计算其夏普比率: 
# 这组收益率是对数收益率,从2006年到2016年,以半年为频率,总共22个数据点
round(df['rtn'].mean()/df['rtn'].std()*np.sqrt(2),3)

输出
0.405

2.4 注意问题

在具体运用中仍需要对夏普比率的适用性加以注意:

• 1.用标准差对收益进行风险调整,其隐含的假设就是所考察的组合构成了投资者投资的全部.因此只有在考虑在众多的基金中选择购买某一只基金时,夏普比率才能够作为一项重要的依据;
• 2.使用标准差作为风险指标也被人们认为不是很合适的.
• 3.夏普比率的有效性还依赖于可以以相同的无风险利率借贷的假设;
• 4.夏普比率没有基准点,因此其大小本身没有意义,只有在与其他组合的比较中才有价值;
• 5.夏普比率是线性的,但在有效前沿上,风险与收益之间的变换并不是线性的.因此,夏普指数在对标准差较大的基金的绩效衡量上存在偏差;
• 6.夏普比率未考虑组合之间的相关性,因此纯粹依据夏普值的大小构建组合存在很大问题;
• 7.夏普比率与其他很多指标一样,衡量的是基金的历史表现,因此并不能简单地依据基金的历史表现进行未来操作.
• 8.计算上,夏普指数同样存在一个稳定性问题: 夏普指数的计算结果与时间跨度和收益计算的时间间隔的选取有关.

尽管夏普比率存在上述诸多限制和问题,但它仍以其计算上的简便性和不需要过多的假设条件而在实践中获得了广泛的运用.

3 最大回撤率

最大回撤率: 在选定周期内任一历史时点往后推,产品净值走到最低点时的收益率回撤幅度的最大值.最大回撤用来描述买入产品后可能出现的最糟糕的情况.最大回撤是一个重要的风险指标,对于对冲基金和数量化策略交易,该指标比波动率还重要,最大回撤是越低越好.

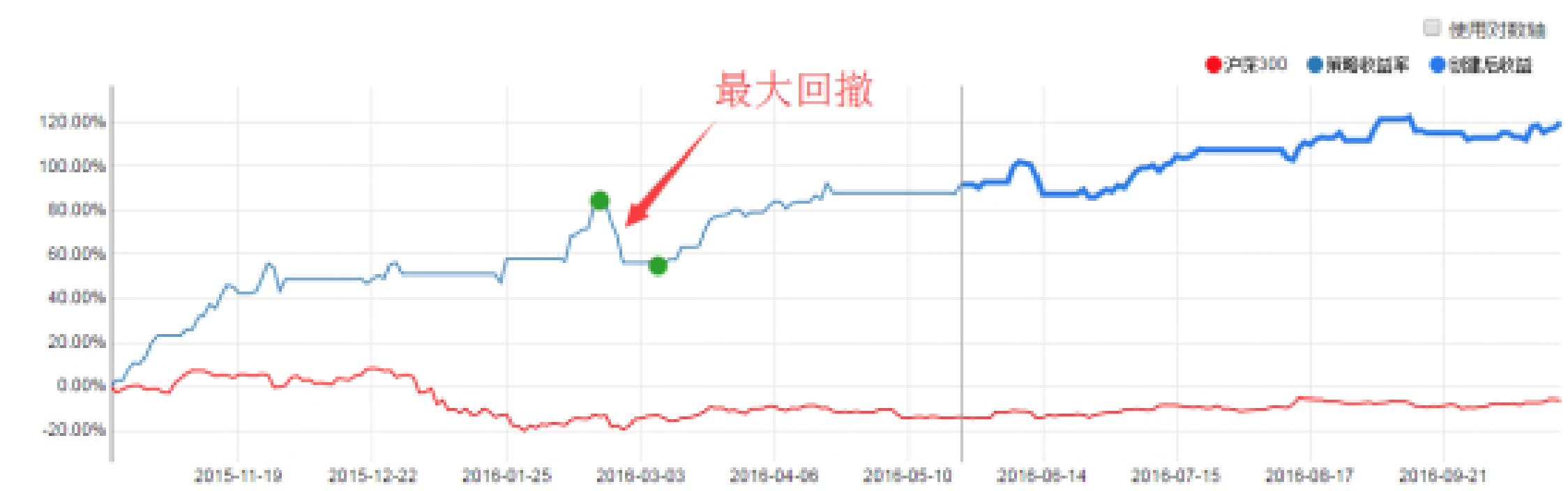
3.1 具体表现

1.回撤用来衡量该私募产品的抗风险能力

2010年7月20日初始净值1;恰逢2010年10月美国推出QE2全球股市大涨,该基金净值增长到1.8;其后国内股市剧烈震荡,截止2011年4月25,该基金净值为0.98.假设投资者在最高峰时期认购,半年后在最低潮时期赎回,亏损45.5%.此就是最大回撤率给高位追买的投资者的指示意义

2.回撤用来描述任一投资者可能面临的最大亏损

一个基金产品用历史绝对收益衡量,它的初始认购者一直持有或许是赚钱的,但是在该私募基金表现最优异时候认购的投资者却不一定赚钱,还甚至有可能巨亏.

比如：一个基金产品成立于2008年11月上证指数1700点初始净值为1,在2009年8月上证指数上涨到3400点时,净值达到2.1,为投资者带来110%回报.在2009-2012持续3年下跌市道中,该基金净值下降到1.2.单从业绩来看,基金依然为投资者创造20%收益,可是若是在2009年8月认购的投资者则亏损幅度达42.8%,而这42.8%就是该基金的最大回撤率.

3.2 计算公式

D为某一天的净值,i为某一天,j为i后的某一天,Di为第i天的产品净值,Dj则是Di后面某一天的净值

drawdown=max((Di-Dj)/Di)

3.3 举个栗子

import pandas as pd
import tushare as ts

start_date='2020-01-01'
end_date='2020-12-16'

def get_max_drawdown(code,start=start_date,end=end_date):  
  df=ts.get_hist_data(code,start=start,end=end)  
  hf=df['close'].max()  
  df['dropdown']=(1-df['close']/hf)  
  max_d=df['dropdown'].max()  
  print('max dropdown of %s is %.2f%s' % (code,max_d*100,'%'))

get_max_drawdown('002049')

输出: 
max dropdown of 002049 is 68.04%

4 贝塔比率(Beta/β)

β系数也称为贝塔系数(Beta coefficient),是一种风险指数,用来衡量个别股票或股票基金相对于整个股市的价格波动情况.β系数是一种评估证券系统性风险的工具,用以度量一种证券或一个投资证券组合相对总体市场的波动性,在股票、基金等投资术语中常见.

• 相当于业绩评价基准收益的总体波动性
• 衡量策略的系统性风险:
  如果Beta为1,策略和市场(参照沪深300指数)同进退
  如果Beta为1.1,市场上涨10%时,策略上涨11%;市场下滑10%时,策略下滑11%.
  如果Beta为0.9,市场上涨10%时,策略上涨9%;市场下滑10%时,策略下滑9%.

那么问题来了, Beta值到底是大好还是小好呢？

这得具体问题具体分析,如果是牛市,股市兴兴向荣,个股、大盘狂涨,那就要选择Beta值大的策略;

如果是熊市,经济下行压力大,就应该选择Beta值小的策略,这样就可以比较好的控制风险,确保资金的安全.

4.1 方法概述

当前,从研究范式的特征和视角来划分,股票投资分析方法主要有如下三种：

• 基本分析
• 技术分析
• 演化分析

这三种分析方法所依赖的理论基础、前提假设、研究范式、应用范围各不相同,在实际应用中它们既相互联系,又有重要区别.

其中基本分析属于一般经济学范式,技术分析属于数理或牛顿范式,演化分析属于生物学或达尔文范式;

基本分析主要应用于投资标的物的选择上,技术分析和演化分析则主要应用于具体操作的时机和空间判断上,作为提高股票投资分析有效性和可靠性的重要手段.

在评估股市波动风险与投资机会的方法中,贝塔系数是衡量结构性与系统性风险的重要参考指标之一,其真实含义就是个别资产及其组合(个股波动),相对于整体资产(大盘波动)的偏离程度.

4.2 基本定义

贝塔系数是统计学上的概念,它所反映的是某一投资对象相对于大盘的表现情况.

其绝对值越大,显示其收益变化幅度相对于大盘的变化幅度越大;

绝对值越小,显示其变化幅度相对于大盘越小.

如果是负值,则显示其变化的方向与大盘的变化方向相反;大盘涨的时候它跌,大盘跌的时候它涨.

由于我们投资于投资基金是为了取得专家理财的服务,以取得优于被动投资于大盘的表现情况,这一指标可以作为考察基金经理降低投资波动性风险的能力.

在计算贝塔系数时,除了基金的表现数据外,还需要有作为反映大盘表现的指标.

根据投资理论,全体市场本身的β系数为1,若基金投资组合净值的波动大于全体市场的波动幅度,则β系数大于1.

反之,若基金投资组合净值的波动小于全体市场的波动幅度,则β系数就小于1.

β系数越大于证券,通常是投机性较强的证券.

以美国为例,通常以标准普尔五百企业指数(S&P 500)代表股市,贝塔系数为1.

一个共同基金的贝塔系数如果是1.10,表示其波动是股市的1.10 倍,亦即上涨时比市场表现优10%,而下跌时则更差10%;

若贝塔系数为0.5,则波动情况只及一半.

β=0.5为低风险股票,

β=1.0表示为平均风险股票,

β=2.0 → 高风险股票,

大多数股票的β系数介于0.5到1.5间.

贝塔系数衡量股票收益相对于业绩评价基准收益的总体波动性,是一个相对指标.

β越高,意味着股票相对于业绩评价基准的波动性越大.

β大于1,则股票的波动性大于业绩评价基准的波动性.反之亦然.

β为1,则市场上涨10%,股票上涨10%;

市场下滑10%,股票相应下滑10%.

如果β为1.1,市场上涨10%时,股票上涨11%;市场下滑10%时,股票下滑11%.

如果β为0.9,市场上涨10%时,股票上涨9%;市场下滑10%时,股票下滑9%.

Beta系数起源于资本资产定价模型(CAPM模型),它的真实含义就是特定资产(或资产组合)的系统风险度量.

所谓系统风险,是指资产受宏观经济、市场情绪等整体性因素影响而发生的价格波动,换句话说,就是股票与大盘之间的联动性,系统风险比例越高,联动性越强.

与系统风险相对的就是个别风险,即由公司自身因素所导致的价格波动.

总风险=系统风险+个别风险

而Beta则体现了特定资产的价格对整体经济波动的敏感性,即市场组合价值变动1个百分点,该资产的价值变动了几个百分点

或者用更通俗的说法:大盘上涨1个百分点,该股票的价格变动了几个百分点.

用公式表示就是：

实际中,一般用单个股票资产的历史收益率对同期指数(大盘)收益率进行回归,回归系数就是Beta系数.

4.3 计算方式

Cov(ra,rm)=ρam*σa*σm
βa=Cov(ra,rm)/(σm^2)
βa=ρam*σa/σm

# ra: 证券a的收益
# rm: 市场收益
# Cov(ra,rm): 证券a的收益与市场收益的协方差
# ρam: 证券a与市场的相关系数
# σa: 证券a的标准差
# σm: 市场的标准差

根据如上公式,贝塔系数并不代表证券价格波动与总体市场波动的直接联系.

不能绝对地说,β越大,证券价格波动σa相对于总体市场波动σm越大;

同样,β越小,也不完全代表σa相对于σm越小.

甚至即使β=0也不能代表证券无风险,而有可能是证券价格波动与市场价格波动无关ρam=0,但是可以确定,如果证券无风险σa,β一定为零.

• 注意：掌握β值的含义

  • β=1,表示该单项资产的风险收益率与市场组合平均风险收益率呈同比例变化,其风险情况与市场投资组合的风险情况一致
  • β>1,说明该单项资产的风险收益率高于市场组合平均风险收益率,则该单项资产的风险大于整个市场投资组合的风险
  • β<1,说明该单项资产的风险收益率小于市场组合平均风险收益率,则该单项资产的风险程度小于整个市场投资组合的风险

一般用途

• 1.计算资本成本,做出投资决策(只有回报率高于资本成本的项目才应投资)
• 2.计算资本成本,制定业绩考核及激励标准
• 3.计算资本成本,进行资产估值(Beta是现金流贴现模型的基础)
• 4.确定单个资产或组合的系统风险,用于资产组合的投资管理,特别是股指期货或其他金融衍生品的避险(或投机)
• 5.贝塔系数在证券市场上的应用

两种模型

• 1.一种是CAPM模型(资本资产定价模型,也称证券市场线模型,security market line)

E(Ri)=Rf+βi(Rm-Rf)

其中：
E(Ri)=资产i的期望收益率
Rf=无风险收益率
Rm=市场平均收益率

• 2.另一种是市场模型

E(Ri)=αi+βiRm

这两个模型都是单变量线性模型,都可用最小二乘法确定模型中的参数.

在这两个模型中,β系数都是模型的斜率.

当αi=Rf(1-βi)时,这两个模型是可以互相转换的.

5 阿尔法比率(Alpha/α)

在当代金融领域,阿尔法代表的最普遍的意思是超额回报.

• 实际收益和按照Beta系数计算的期望收益之间的差额.
• 代表策略多大程度上跑赢了预期的收益率

5.1 计算公式

阿尔法系数=投资的实际回报率-市场无风险利率-贝塔系数*市场回报

5.2 举个例子：

一个投资沪深300的基金,2016年的实际收益率为9%,那么它的阿尔法系数α=9%-1.5%-1*5.6%=1.9

这个阿尔法系数在计算时,市场无风险利率是以中国一年期定存利率为标准,默认贝塔是1,5.6%是沪深300在2015年的涨幅.

如果阿尔法大于0(α>0),则说明这只基金还可以,阿尔法小于0(α<0),买这个基金还不如银行定存.

其实如果股市跌的一塌糊涂,阿尔法及时很高,收益率也是负的.但是并不代表这只基金不好,阿尔法越高,这个基金相对于银行存款来说就越适合投资.

import pandas as pd
import tushare as ts
import matplotlib.pyplot as plt

start_date='2020-01-01'
end_date='2020-12-16'

def calculate_beta(df_stock,df_hs300,code,start=start_date,end=end_date):  
  df=pd.DataFrame({code:df_stock['close'].pct_change(),'hs300':df_hs300['close'].pct_change()},index=df_stock.index)
  cov=df.corr().iloc[0,1]
  df_hs300['change']=df_hs300['close'].pct_change()*100
  var=df_hs300['change'].var()
  beta=cov/var
  return beta

# 定价曲线
def make_capm(code,start=start_date,end=end_date):
  df_stock=ts.get_hist_data(code,start=start,end=end)
  df_hs300=ts.get_hist_data('hs300',start=start,end=end)
  df_stock.sort_index(ascending=True,inplace=True)
  df_hs300.sort_index(ascending=True,inplace=True)
  beta=calculate_beta(df_stock,df_hs300,code,start=start,end=end)
  loss_free_return=0.04
  df=pd.DataFrame({code:df_stock['close']/df_stock['close'].values[1]-1,
           'hs300':df_hs300['close']/df_hs300['close'].values[1]-1,
           'days':range(1,df_stock.shape[0]+1)},index=df_stock.index)
  df['beta']=df['days']*loss_free_return/250 + beta*(df['hs300']-df['days']*loss_free_return/250)
  df['alpha']=df[code]-df['beta']
  df[[code,'hs300','beta','alpha']].plot(figsize=(960/72,480/72))

make_capm('600519')
plt.show()